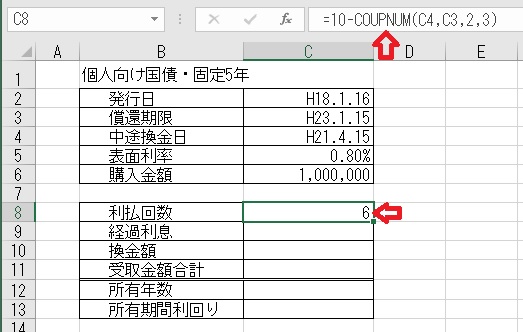
上記のセルC8に「=10−COUPNUM(C4,C3,2,3)」と入力すると、
「利払回数」が求められる。

上記にセルC9に
「=IF(C8<4," ",ROUND(COUPDAYBS(C4,C3,2,3)*C5/365*C6,0))」と
入力すると、「経過利息」が求められる。

上記のセルC10に「=IF(C9=" " ," ",C6+C9−4*C6*C5/2*80%)」と
入力すると、「換金額」が求められる。

上記のセルC11に「=C10+C6*C5/2*C8」と入力すると、「受取金額合計」
が求められる。
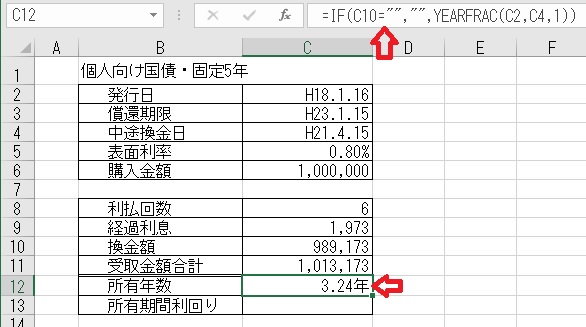
上記のセルC12に「=IF(C10=" "," ",YEARFRAC(C2,C4,1))」と入力すると、
「所有年数」が求められる。

上記のセルC13に「=(C11−C6)/C6/C12」と入力すると、「所有期間利回り」
が求められる。
287.COUPDAYBS関数、COUPNUM関数、YEARFRAC関数で、国債の所有期間の
利回りを求める。
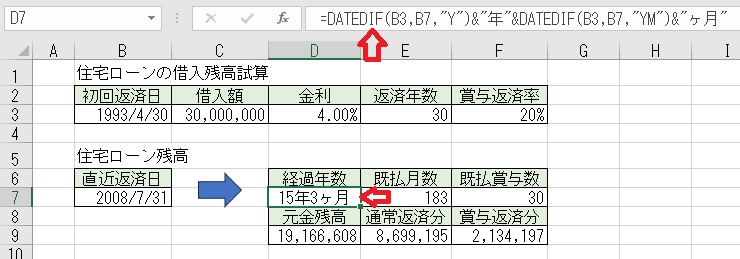
上図のセルD7に「=DATADIF(B3,B7,"Y")&"年"&DATEDIF(B3,B7,"YM")&"ケ月"」
と入力すると、ローン支払いの「経過年数」が求められる。
DATEDIF関数の引数は、「=DATEDIF(開始日,終了日,単位)」となり、「単位」は
下表の様になり、日付間の期間数を指定した単位で求める。

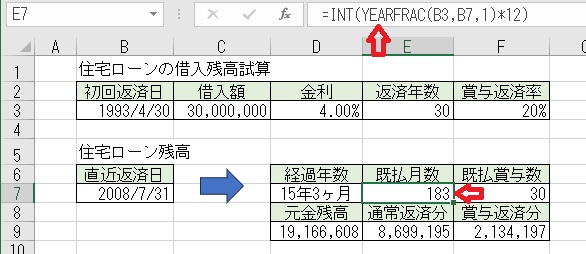
上図のセルE7に「=INT(YEARFRAC(B3,B7,1)*12)」と入力すると、
「既払月数」が求められる。
YEARFRAC関数の引数は、「=YEARFRAC(開始日,終了日,基準)」となり、
「基準は」下表より指定する。

尚、NASD方式とは1ケ月を30日とする計算式である。
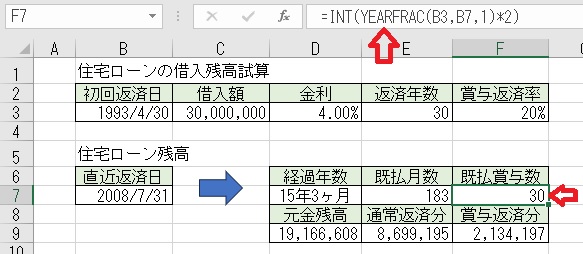
上記のセルF7に「=INT(YEARFRAC(B3,B7,1)*2)」と入力すると、
「既払賞与数」が求められる。
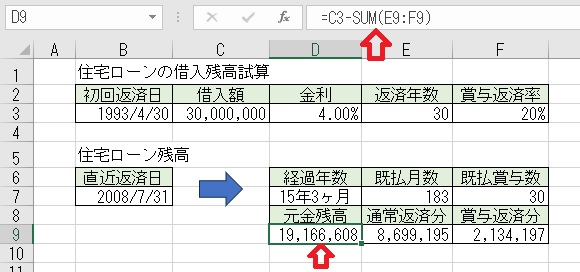
上図のセルD9に「=C3−SUM(E9:F9)」と入力すると、「元金残高」が求め
られる。

上記のセルE9に「=CUMPRINC(D3/12,E3*12,C3*(1−F3),1,E7,0)」と入力
すると、「通常返済分」が求められる。
CUMPRINC関数は、元利均等払いの特定期間の「元金」合計を返す関数である。
CUMPRINC関数の引数は「=COMPRINC(利率,期間,現在価値,開始期,終了期,
支払期日)」と指定する。
引数の「現在価値」の「C3*(1−F3)」は「借入額」から「賞与返済分」を引い
た額になる。「開始期」に「1」を、「終了期」に「既払月数」を、「支払期間」
は「期首払い」なら「1」を、「期末払い」なら「0」を指定する。

上記のセルF9に「=−CUMPRINC(D3/2,E3*2,C3*F3,1,F7,0)」と入力すると、
「賞与返済分」が求められる。286.DATEDIF関数、CUMPRINC関数、YEARFRAC関数で、住宅ローンの借入残高を
試算する。
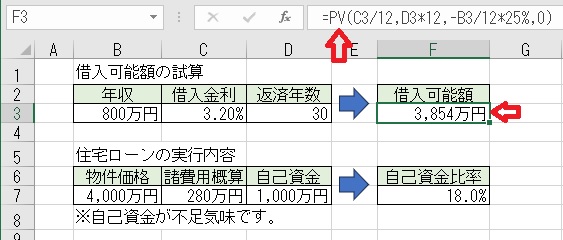
上記のセルF3に「=PV(C3/12,D3*12,−B3/12*25%,0)」と入力すると、
「借入可能額」が求められる。
この住宅ローンの返済は、年収の25%以内にあたる金額を返済に充てるとして
算出すると、「B3/12*25%」として、年収を12で割った月収の25%を定期的
に返済するものとして「借入可能額」を算出する。
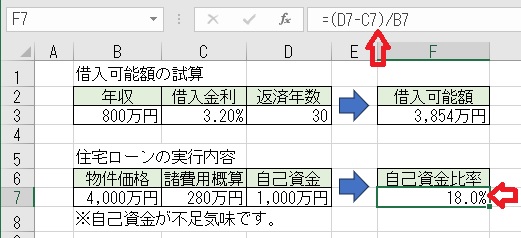
上図のセルF7に「=(D7−C7)/B7」と入力すると、自己資金比率が求められる。

上図のセルB8に「=IF(F7<0,"※諸経費を支払うための自己資金が不足しています。",IF(F7<20%,"※自己資金が不足気味です。","
"))」と入力すると、自己
資金の状態を判定する。
実際にマイホームを購入する場合は、一般的に登記費用や頭金などを含めた
「自己資金」が現金で必要になる。この自己資金は、購入物件の約20%を用意
する必要がある。
そこで、「(自己資金−諸経費)÷物件価格」としてF7セルで率を計算し、この率
が20%より低い場合は、メッセージを表示させている。
285.PV関数で、借入可能額を求める。
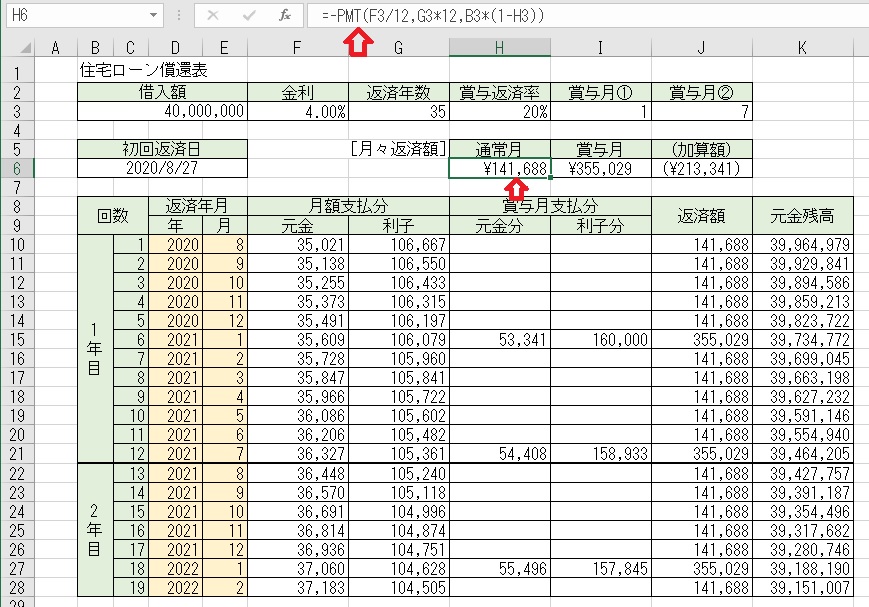
上図のセルH6に「=−PMT(F3/12,G3*12,B3*(1−H3))」と入力すると、
月々の返済額の内の「通常月」の返済額が求められる。
PMT関数の引数は、「=PMT(金利,返済回数,借入額)」である。
「B3*(1−H3)」の記述は、「B3×H3=8,000,000」となり「賞与返済額」が
800万円で「借入額」から「賞与返済額」をマイナスした「3,200万円」が
「通常月」の「借入額」となる。
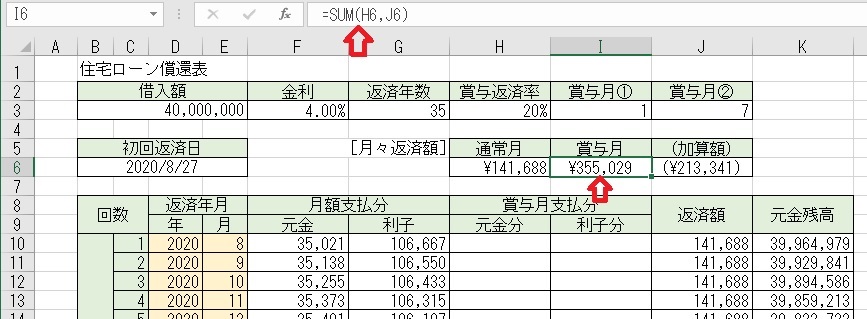
上図のセルI6に「=SUM(H6,J6)」と入力すると、「賞与月」の返済額が求めら
れる。
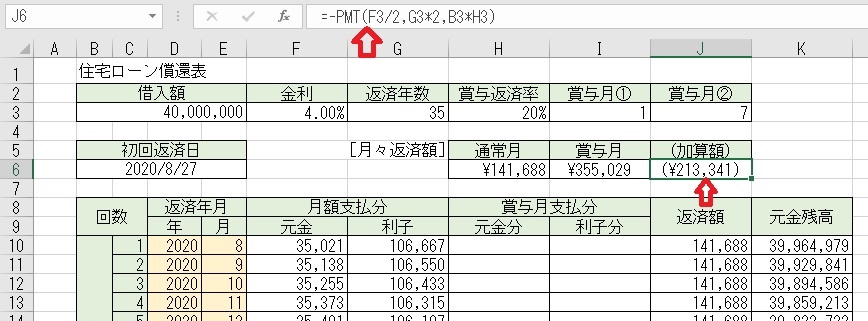
上図のセルJ6に「=−PMT(F3/2,G3*2,B3*H3)」と入力すると、賞与月の
「加算額」が求められる。
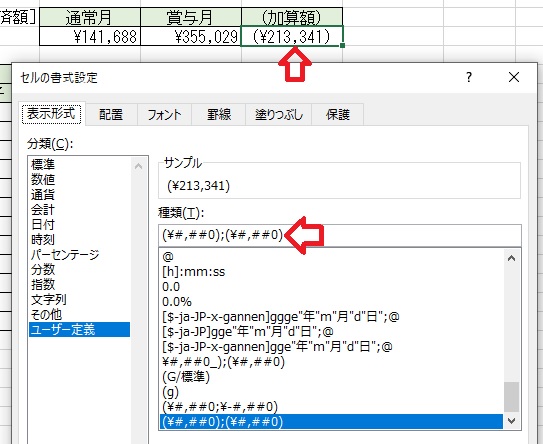
尚、「加算額」の様に金額をカッコで囲みたいようなときは、下図のように
[ユーザー定義]の種類でカッコを付ける。
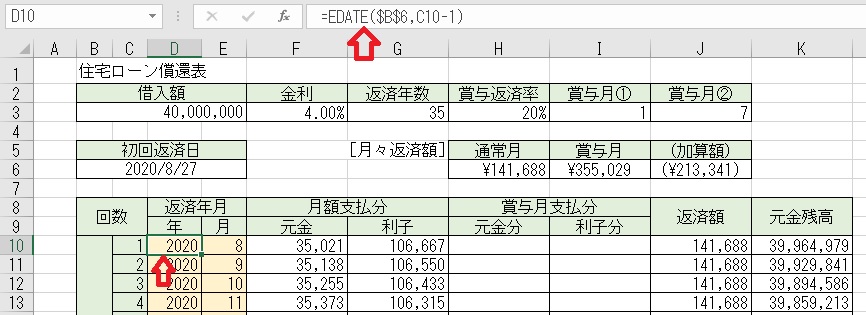
上図のセルD10に「=EDATE($B$6,C10−1)」と入力すると、「初回返済日」
から「返済回数」に対する日付関数が取り出せる。
「=EDATE(B6,C10−1)」=「44070」となる。
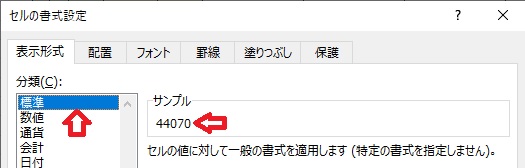
[表示形式]で[標準]にすると、日付関数が表示できる。

「2020」と表示するためには、上記の様に設定する。
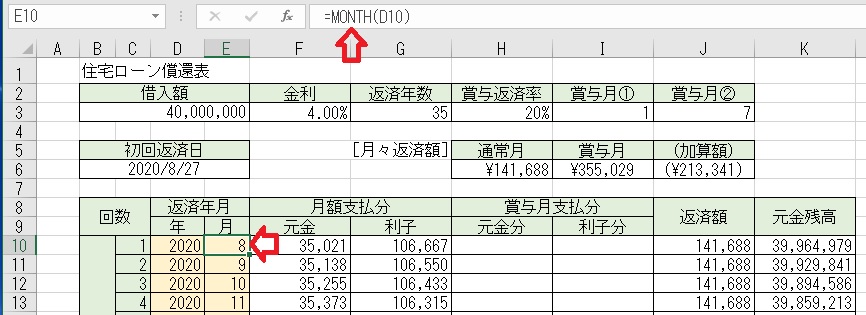
上図のセルE10に「=MONTH(D10)」と入力すると、月が取り出せる。
MONTH関数で、セルD10の日付関数から月数だけを取り出している。
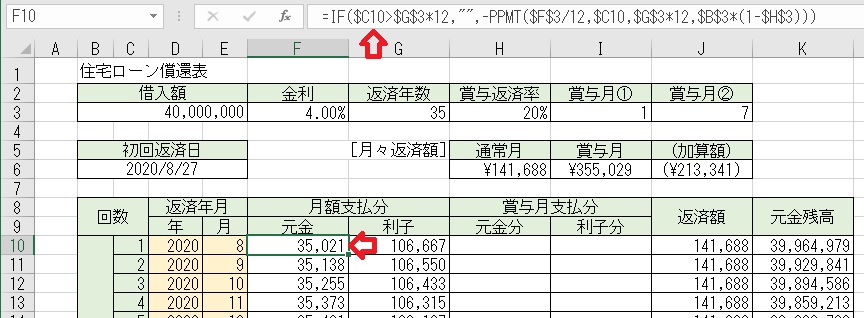
上図のセルF10に「=IF($C10>$G$3*12," ",−PPMT($F$3/12,$C10,$G$3*
12,$B$3*(1−$H$3)))」と入力すると、「返済回数」に対する「月額支払分」
が求められる。
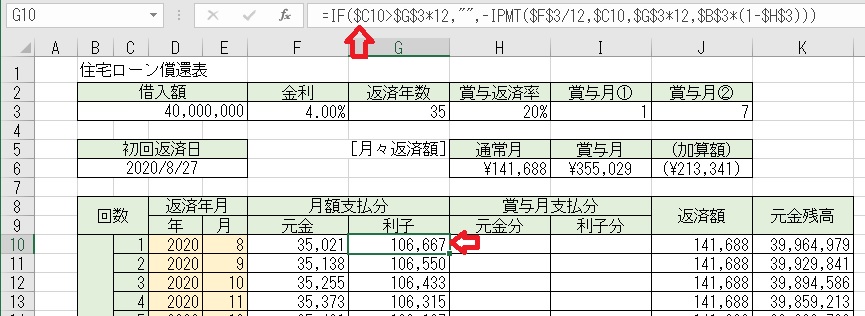
上図のセルG10に「=IF($C10>$G$3*12," ",−IPMT($F$3/12,$C10,$G$3*
*12,$B$3*(1−$H$3)))」と入力すると、「返済回数」に対する「月額支払分」
による「返済利子分」が求められる。
「元金」と「利子」を求める式は同じで、PPMT関数が「元金」を求めて、
IPMT関数が「利子」を求める。

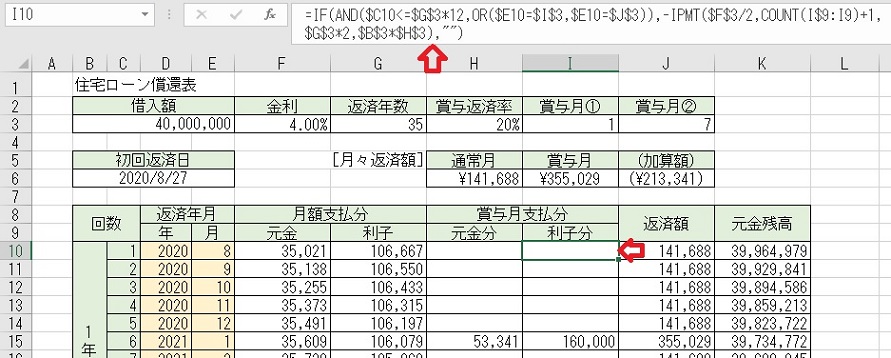
上図のセルH10に「=IF(AND($C10<=$G$3*12,OR($E10=$I$3,$E10=$J$3)),
−PPMT($F$3/2,COUNT(H$9:H9)+1,$G$3*2,$B$3*$H$3)," ")」と入力する
と、「返済回数」に対する「賞与月支払分」による「元金返済分」が求められる。
PPMT関数の部分で、第2引数の「期」にあたる部分は、ボーナス払いは何回目の
支払いかを数えて指定する必要があるが、ここではCOUNT関数を使って、上の行
までの件数を数えている。
上図のセルI10に「=IF(AND($C10<=$G$3*12,OR($E10=$I$3,$E10=$J$3)),
−IPMT($F$3/2,COUNT($I9:I9)+1,$G$3*2,$B$3*$H$3)," ")」と入力する
と、「返済回数」に対する「賞与月支払分」による「利子返済分」が求められる。
1月と7月以外は支払が無いので表示されない。

上記のセルJ10に「=IF(F10=" "," ",SUM(F10:I10))」と入力すると、その月の
「返済額」が求められる。
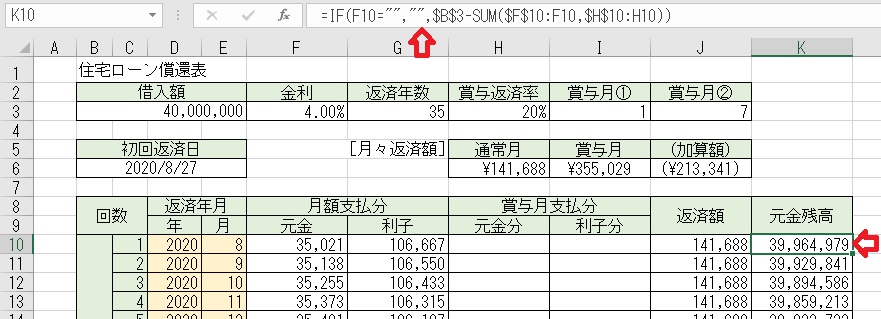
上記のセルK10に「=IF(F10=" "," ",$B$3−SUM($F$10:F10,$H$10:H10))」と
入力すると、その「返済回」の「元金残高」が求められる。
C列の回数を最後まで下に入れて、その行までD列からK列までをコピーすれば完成
である。
284.IPMT関数、PMT関数、PPMT関数、EDATE関数、MONTH関数で住宅ローン
の償還表を作成する。

上図のセルD6に「=ROUNDUP(NPER(E3/12,−F3,D3),0)」と入力すると、
「返済回数」が求められる。
NPER関数は、「NPER(利率,定期支払額,借入額)」として指定する。
「利率」は月払いなので、12で割って月利にする。「定期支払額」は負の値
でマイナスになる。

上図のセルC8に「=IF(B8>$D$6," ",SUM(D8:E8))」と入力すると、
「返済月額」が求められる。
IF関数で「返済回数」と比較して「回数」が超えると空白になる。
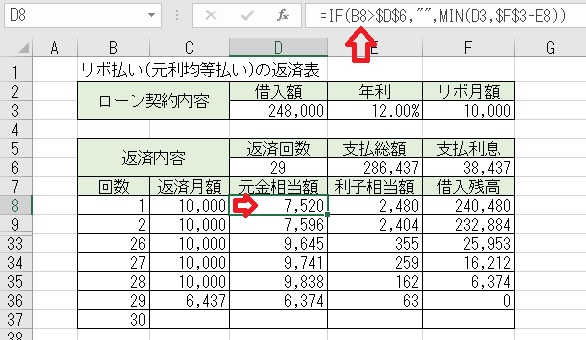
上図のセルD8に「=IF(B8>$D$6," ",MIN(D3,$F$3−E8))」と入力する
と、「その回数目」の「返済月額」に対する「元金相当額」が求められる。
「元金相当額」は「リボ月額−利子相当額」で求められるが、当初は「借入
額」の方が少ない場合もあるので、MIN関数で少ない方を表示させている。

上図のセルE8に「=IF(B8>$D$6," ",INT(D3*$E$3/12))」と入力する
と、「利子相当額」が求められる。
利子は「残高×利率÷12」として求められるが、1回目分は「借入額×利率
÷12」で求められる。
INT関数は、小数点以下を切り捨てて整数だけを取得している。

上図のセルF8に「=IF(D8=" "," ",$D$3−SUM($D$8:D8))」と入力する
と、「借入残高」が求められる。
「借入残高」は「借入額−元金相当額の合計」として求められる。
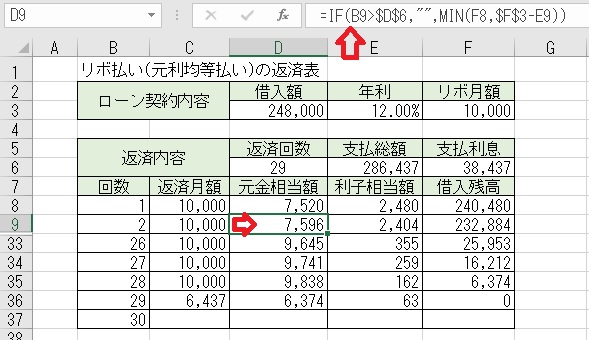
上図のセルD9に「=IF(B9>$D$6," ",MIN(F8,$F$3−E9))」と入力する
と、2回目以降の「元金相当額」が求められる。
2回目以降の「元金相当額」は「借入額」ではなく「借入残高」を参照し
て、「0」になれば終わりである。
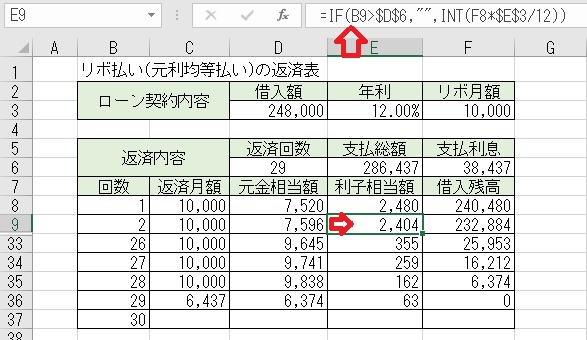
上図のセルE9に「=IF(B9>$D$6," ",INT(F8*$E$3/12))」と入力する
と、2回目以降の「利子相当額」が求められる。
2回目以降の「利子相当額」は「借入額」ではなく「借入残高」を参照して
「0」になれば終わりである。
尚、セルD9からE9を下の行にコピーすれば、最数回までの値が求められる。

上図のセルE6に「=SUM(C8:C36)」と入力すると、「支払総額」が求めら
れる。
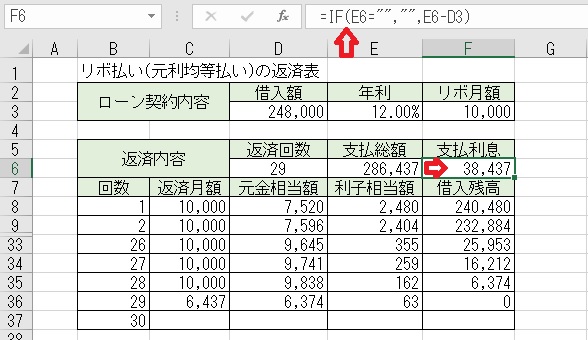
上図のセルF6に「=IF(E6=" "," ",E6−D3)」と入力すると、「支払利息」が
求められる。
283.ROUNDUP関数、NPER関数、MIN関数、IF関数で、元利均等タイプの
リボ払いの返済表を作成する。
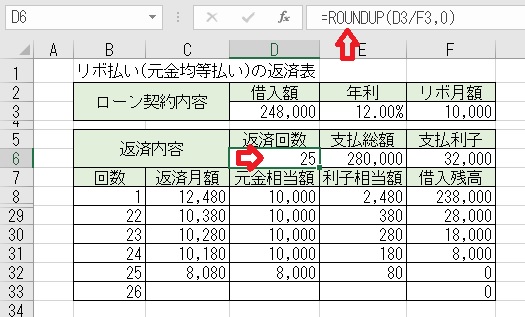
上記のセルD6に「=ROUNDUP(D3/F3,0)」と入力すると、「返済回数」が
求められる。ROUNDUP関数で、結果の端数を切り上げている。
「リボ払い」は、クレジットカードなどの決済方法のひとつで、毎月の返済額
が一定となるタイプである。リボ払いは、毎月の「元金」が一定額のタイプと
「元利」が一定額のタイプがある。
ここでは「元金」が一定のタイプの明細一覧表を作成する。
リボ払いの場合「返済回数」は諸条件によって決まるので、まず上図のセルD6
の様に求める。基本的に、元金均等タイプの場合は、「借入額÷リボ月額」で
決まるが、端数が生じる場合があるので、ROUNDUP関数で端数を切り上げて
いる。

上図のセルC8に「IF(B8>$D$6," ",SUM(D8:E8))」と入力すると、回数目の
「返済月額」が求められる。「返済月額」は「元金」と「利子」の合計である。
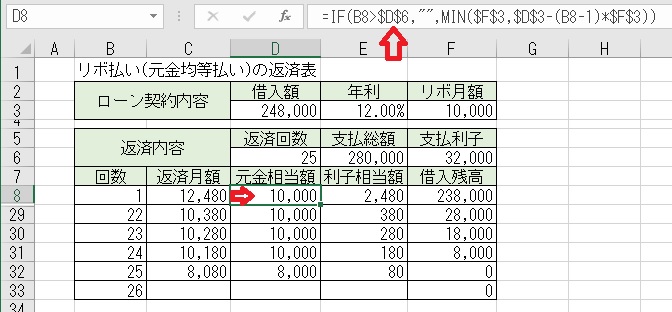
上図のセルD8に「=IF(B8>$D$6," ",MIN($F$3,$D$3−(B8−1)*$F$3))」
と入力すると、「リボ月額」に対する「元金相当額」が求められる。
元金は、基本的に「リボ月額」となるが、端数が生じるために、MIN関数を
使ってリボ月額のF3セルと「D3−(B9−1)*F3」で計算できる残高を比べて
少ない方を表示している。先頭のIF関数は、D6セルの「返済回数」を超えて
いる場合には、何も表示させないためのものである。
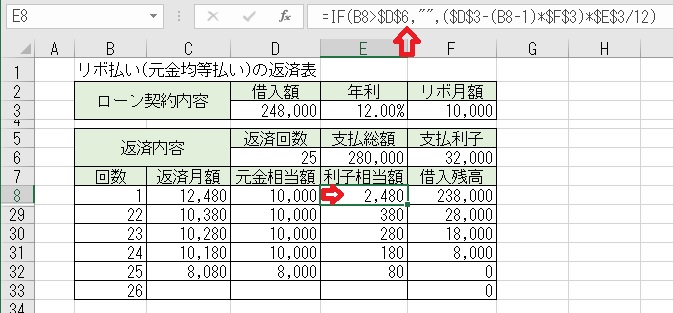
上記のセルE8に「=IF(B8>$D$6," ",($D$3−(B8−1)*$F$3)*$E$3/12)」
と入力すると、「リボ月額」に対する「利子相当額」が求められる。
利子は、「残高×年利÷12」として計算している。
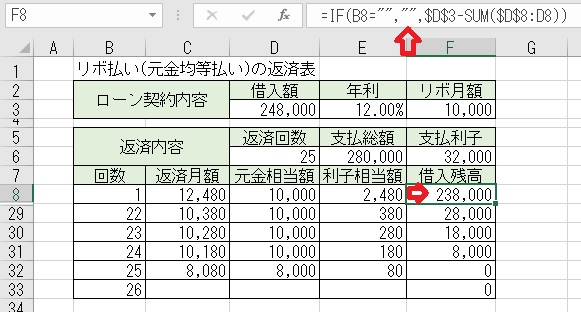
上図のセルF8に「=IF(B8=" "," ",$D$3−SUM($D$8:D8))」と入力すると、
「1回目」の「借入残高」が求められる。
「借入残高」は「借入額−元金相当額の合計」として求められる
セルC8からF8までを下にコピーすると、最終回まで計算することができる。
「支払総額」は「=SUM(C8:C33)」として求められ、
「支払利子」は「=E6−D3」として求められる。
282.ROUNDUP関数、MIN関数、IF関数で、元利均等タイプのリボ払いの
返済表を作成する。
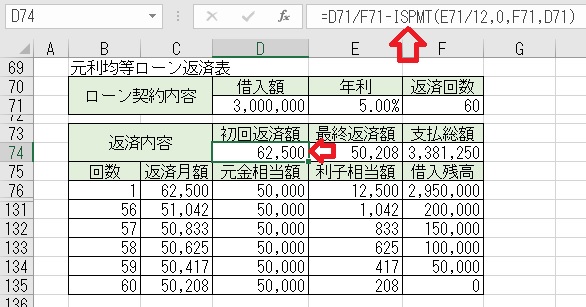
上図のセルD74に、「=D71/F71−ISPMT(E71/12,0,F71,D71)」と入力する
と、「初回返済額」が求められる。元利均等払いの場合は、毎回の返済額が変
わる為、まず「初回返済額」と「最終返済額」を求めておく。
返済額は「元金+利子」で計算でき、その内の「元金」は「借入額÷返済回数」
で計算できる。「利子」はISPMT関数で求められる。
計算結果は、支出としてマイナスになるので、「−ISPMT」として加算できる
ようにしている。
ISPMT関数で、「期末払い」の金額を求めるには「回数−1」と指定すればよい
ので、初回は「1−1」で「0」、最終回は「返済回数−1」で計算できる。
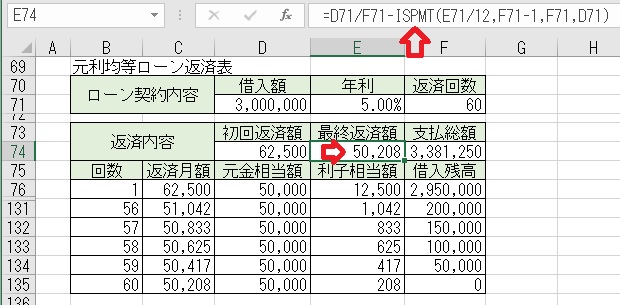
上図のセルE74に「=D71/F71−ISPMT(E17/12,F71−1,F71,D17)」と入力
すると、「最終返済額」が求められる。
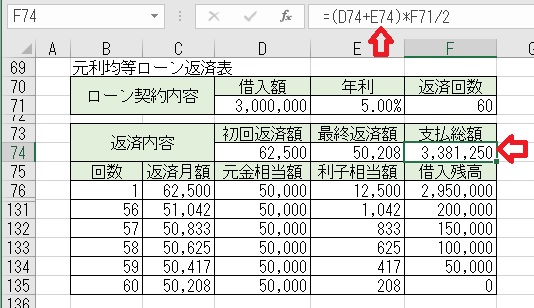
上図のセルF74に「=(D74+E74)*F71/2」と入力すると、「支払総額」が
求められる。
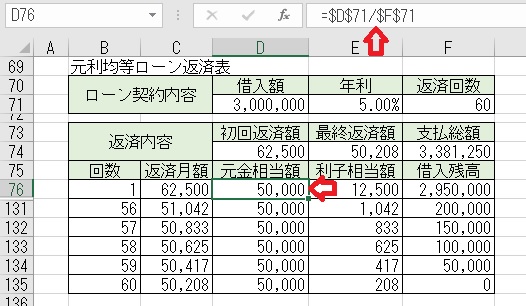
上図のセルD76に「$D$71/$F$71」と入力すると、「返済回数目」の
「元金相当額」が求められる。
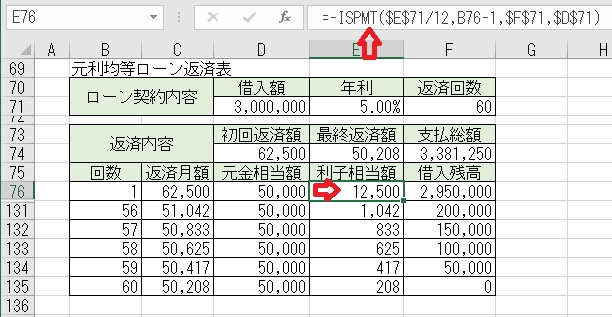
上図のセルE76に「=−ISPMT($E$71/12,B76−1,$F$71,$D$71)」と入力
すると、「返済回数目」の「利子相当額」が求められる。
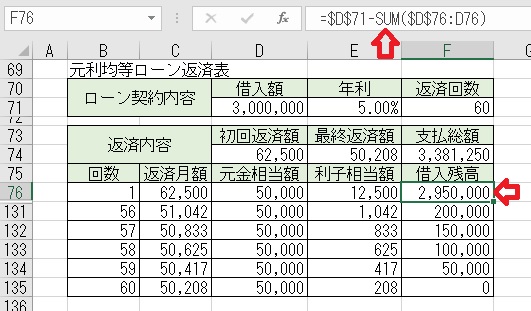
上記のセルF76に「=$D$71−SUM($D$76:D76)」と入力すると、
「返済回数目」の「借入残高」が求められる。
セルC76からF76までの計算式を、下部60回までコピーすると表が完成する。
上図は、2回目から55回目までは非表示になっている。
281.ISPMT関数で、元利均等払いの返済表を作成する。

上図のセルD6に、「=−PMT(E3/12,F3,D3)」と入力すると、「返済月額」が
求められる。
「支払総額」=「返済月額」×「返済回数」
「支払利子」=「支払総額」−「借入額」
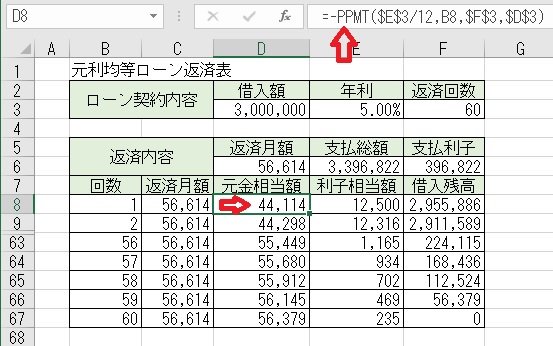
上図のセルD8に、「=−PPMT($E$3/12,B8,$F$3,$D$3)」と入力すると、
「返済月額」の内の「元金相当額」が求められる。
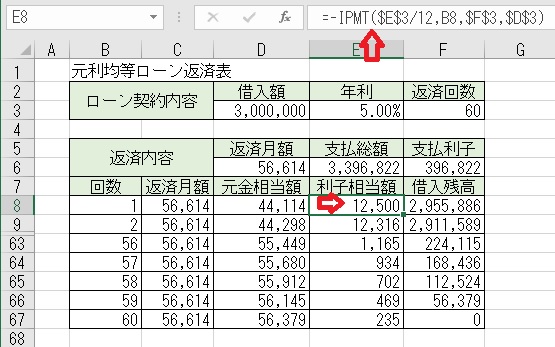
上図のセルE8に、「=−IPMT($E$3/12,B8,$F$3,$D$3)」と入力すると、
「返済月額」の内の「利子相当額」が求められる。
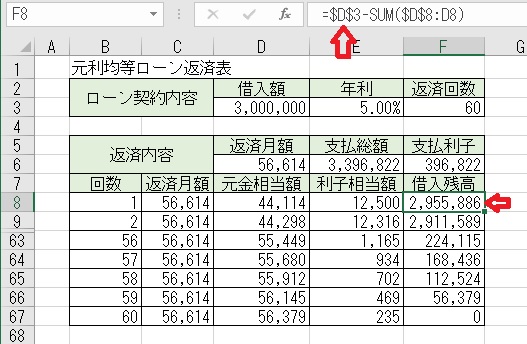
上図のセルF8に「=$D$3−SUM($D$8:D8)」と入力すると、「返済回数目」
時点の「借入残高」が求められる。
尚、この表は行8から行67まで入力してあり、9行目から63行目までは非表示
になっている。「=$D$3−SUM($D$8:D8)」を非表示のセルにもコピーして
あるので、再表示にすれば60回目までの返済回数ごとの「元金相当額」「利子
相当額」「借入残高」を見ることができる。
280.IPMT関数、PMT関数、PPMT関数で、元利均等払いの返済表を作成する。
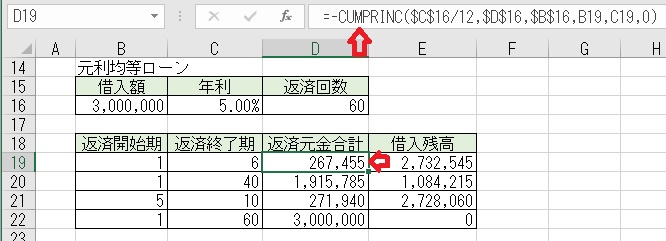
上図のセルD19に、「=−CUMPRINC($C$16/12,$D$16,$B$16,B19,C19,0,)」
と入力すると、「返済開始期」1回目から「返済終了期」6回目までの
「返済元金合計」が求められる。
「借入残高」は「借入額」−「返済元金合計」となる。
CUMPRINC関数の書式は
「=CUMPRINC(利率,期間,現在価値,開始期,終了期,支払期日)」となる。
「現在価値」は、ローン計算では借入総額を正の値で指定する。
「支払期日」は「期首払い」なら「1」、「期末払い」なら「0」を指定する。
279.CUMPRINC関数で、元利均等払いの指定期間の「元金合計」と「借入残高」
を求める。
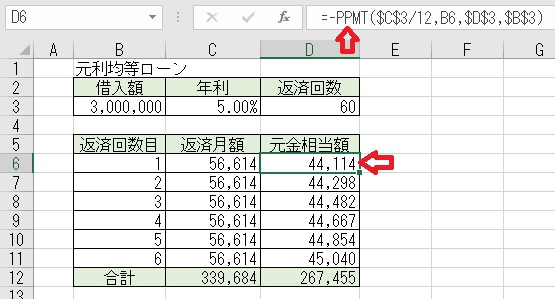
上図のセルD6に、「=−PPMT($C$3/12,B6,$D$3,$B$3)」と入力すると、
「返済回数目」の返済金額の内の「元金相当額」が求められる。278.PPMT関数で、元利均等払いの指定期間の「元金」合計を求める。
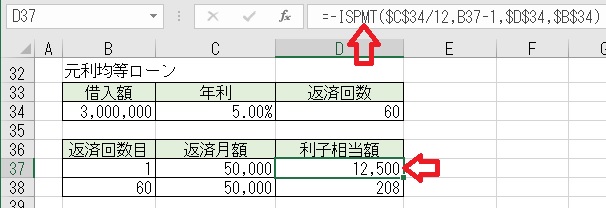
上図のセルD37に「=−ISPMT($C$34/12,B37−1,$D$34,$B$34)と入力すると、
「返済回数目」の「利子相当額」が求められる。
「元利均等払い」は、毎回の元金相当分の支払い額が一定で、その時点の借入残高
に応じた利子相当額を上乗せする返済方法である。
そのため、利子相当額は当初の方が大きくなる。
ISPMT関数の書式は、「=ISPMT(金利月利,返済回数目−1,返済回数,借入額)」と
なる。尚、「期末払い」で計算する場合は、「返済回数目」に「−1」を指定する。
277.ISPMT関数で、元利均等払いの「利子」相当額を求める。
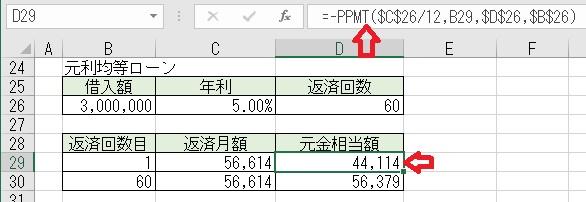
上図のセルD29に「=−PPMT($C$26/12,B29,$D$26,$B$26)」と入力すると、
「返済回数1回目」の「返済月額」の内「元金相当額」が求められる。
PPMT関数の書式は、「PPMT(月額金利,返済回数目,返済回数,借入額)」となる。
276.PPMT関数で、元利均等払いの「元金」相当額を求める。

上図のセルD20に「=−IPMT($C$17/12,B20,$D$17,$B$17)」と入力すると、
「利子相当額」が求められる。
元利均等払いの場合は、最初の内は「利子相当額」の割合が大きく、だんだん
元金の割合が増えてゆく。この各回の利子相当分の計算ができるのがIPMT関数
である。
IPMT関数の書式は、「=IPMT(月額金利,返済回数目,返済回数,借入額)」である。
計算結果がマイナスで返されるので、先頭にマイナスを付けてプラス表示にして
いる。又、返済が毎月なので、年利は12で割って月利にしている。
275.IPMT関数で、元利均等払いの「利子」相当額を求める。
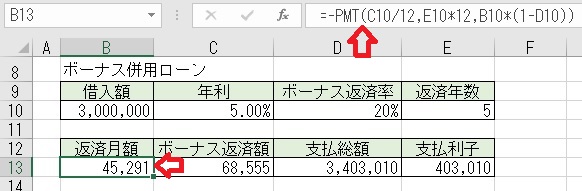
上図のセルB13に「=−PMT(C10/12,E10*12,B10*(1−D10))」と入力すると、
「返済月額」が求められる。
ボーナス返済額は「=−PMT(C10/2,E10*2,B10*D10)」となる。
支払総額は「=((B13*12)+(C13*2))*E10)」となる。
支払総額は「=返済月額*12*返済年数+ボーナス返済額*2*返済年数」という
ことになる。
但し、ボーナスが年2回出たらということになる。
274.PMT関数で、ボーナス併用ローンの返済額を求める。
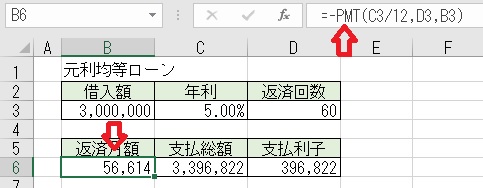
上図のセルB6に「=−PMT(C3/12,D3,B3)」と入力すると、毎月の「返済額」が
求められる。
PMT関数の引数は、「=PMT(金利,返済回数,借入額)」で返済としてマイナスで
返されるので、先頭にマイナスを付けてプラス値になるようにしている。
支払総額=月返済額×返済回数
支払利息=支払総額−借入額
273.PMT関数で、元利均等払いのローン返済額を求める。
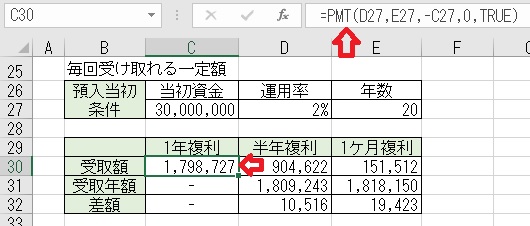
上図のセルC30に、「=PMT(D27,E27,−C27,0,TRUE)」と入力すると、
「1年複利」での「年に1回」受け取り額が求められる。

上図のセルD30に、「=PMT(D27/2,E27*2,−C27,0,TRUE)」と入力すると、
「半年複利」での「半年に1回」受け取れる金額を求められる。
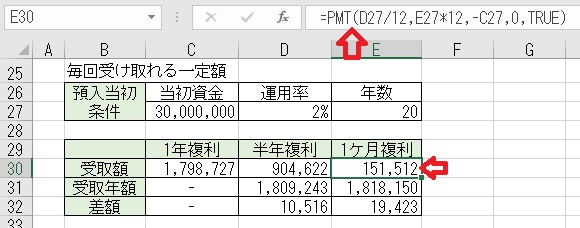
上図のセルE30に、「=PMT(D27/12,E27*12,−C27,0,TRUE)」と入力すると、
「1ケ月複利」での「月に1回」受け取れる金額を求められる。
272.PMT関数で、資金を切り崩す際の毎回受け取れる金額を求める。
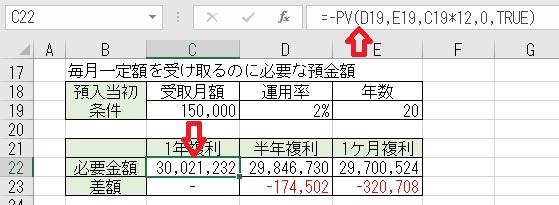
上図のセルC22に、「=−PV(D19,E19,C19*12,0,TRUE)」と入力すると、
「運用率」2%で「1年複利」の運用で「20年間」「月額」150,000円受け取る
ための預金額が求められる。
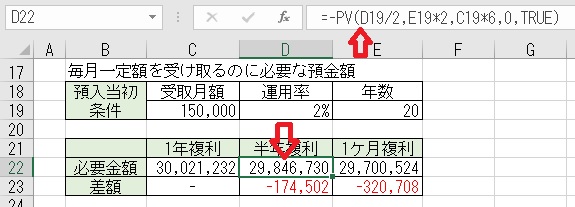
上図のセルD22に「=−PV(D19/2,E19*2,C19*6,0,TRUE)」と入力すると、
「半年複利」の運用で「20年間」「月額」150,000円受け取るための預金額
が求められる。
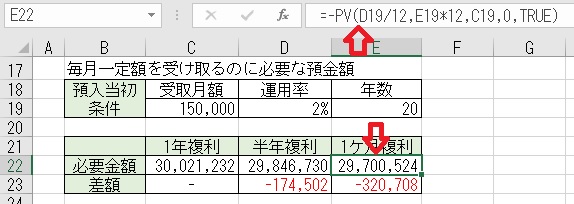
上図のセルE22に「=−PV(D19/12,E19*12,C19,0,TRUE)」と入力すると、
「1ケ月複利」の運用で「20年間」「月額」150,000円受け取るための預金額
が求められる。
PV関数の引数は「=−PV(利率,期間,定期支払額)」で、計算結果が投資として
マイナスで返るので、プラスの値に換算するために先頭に「−」を指定する。
一定額を切り崩しながら、老後の生活費の一部に割り当てる計算方法を「年金計
算」と呼び、一定額を一定期間受け取るために、当初必要となる金額の計算方法
である。271.PV関数で、毎月一定額を受け取るのに必要な預金額を求める。
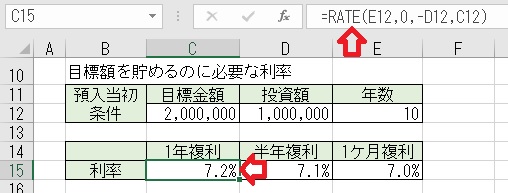
上図のセルC15に、「=RATE(E12,0,−D12,C12)」と入力すると、目標額を
貯めるために必要な「1年複利」の場合の利率を求められる。
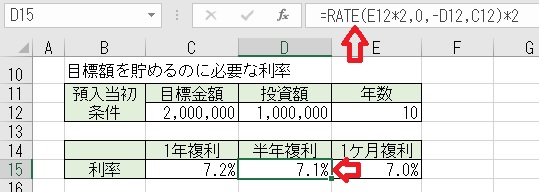
上図のセルD15に「=RATE(E12*2,0,−D12,C12)*2」と入力すると、目標額
を貯めるために必要な「半年複利」の場合の利率を求められる。
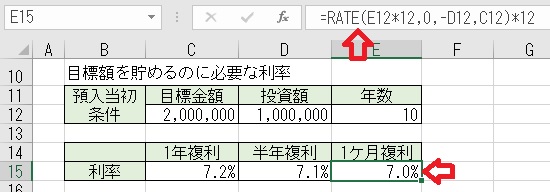
上図のセルE15に「=RATE(E12*12,0,−D12,C12)*12」と入力すると、目標
額を貯めるために必要な「1ヶ月複利」の場合の利率を求められる。
RATE関数の引数は「=RATE(期間,定期支払額,現在価値,将来価値」となり、
第2引数の「定期支払額」はないので「0」で指定し、第3引数の「現在価値」は
投資としてマイナスで指定する。第4引数の「将来価値」は「目標金額」になる。
270.RATE関数で、目標額をためるのに必要な利率を求める。
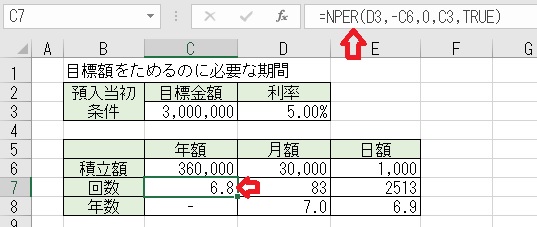
上図のセルC7に「=NPER(D3,−C6,0,C3,TRUE)」と入力すると、目標額を
貯めるのに必要な回数(期間年)が求められる。
NPER関数の引数は、「=NPER(利率,定期支払額,現在価値,目標金額,支払期日)」
となる。第2引数の「定期支払額」はマイナスにする。第3引数の「現在価値」
は「0」に、第5引数の「支払期日」は期首払いとして「TRUE」を指定する。
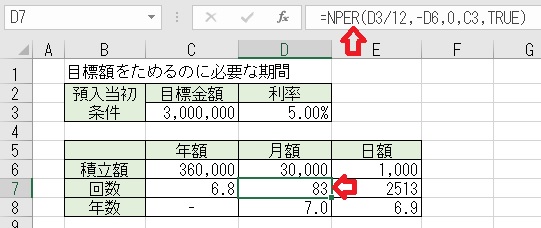
上図のセルD7に「=NPER(D3/12,−D6,0,C3,TRUE)」と入力すると、目標額を
貯めるために必要な回数(期間月)が求められる。
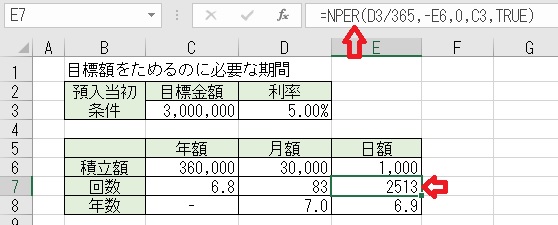
上図のセルE7に「=NPER(D3/365,−E6,0,C3,TRUE)」と入力すると、目標額を
貯めるために必要な回数(期間日)が求められる。
269.NPER関数で、目標額を貯めるのに必要な期間を求める。
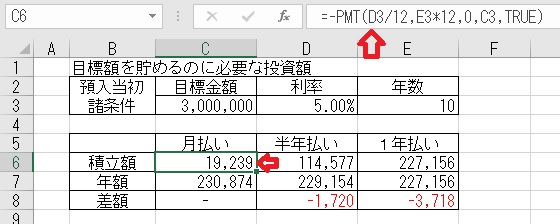
上図のセルC6に、「=−PMT(D3/12,E3*12,0,C3,TRUE)」と入力すると、
月払いの積立額が算出される。
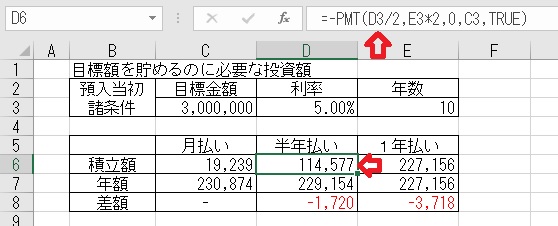
上図のセル、D6に「=−PMT(D3/2,E3*2,0,C3,TRUE)」と入力すると、
半年払いの積立額が算出される。
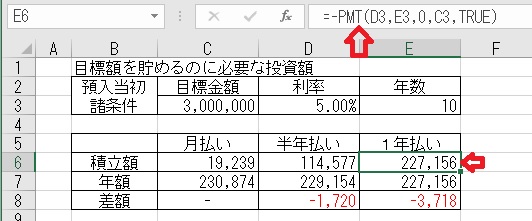
上図のセルE6に、「=−PMT(D3,E3,0,C3,TRUE)」と入力すると、1年払いの
積立額が算出される。
PMT関数は、目標額に対して一定額を積立て貯める場合に、必要になる毎回の
積立額を求めることができる。
一般的な月払いの場合は、「利率」を「12」で割って「月利」にし、期間=回数
を「年数×12」と指定する。このような「積立額」を毎月「支出」するために、
計算結果はマイナスで求められるので、先頭に「−」を付けてプラス値に換算し
ている。最後の引数に「TRUE」を指定して「期首払い」としている。

図のように、「期首払い」の場合は「半年払い」や「年払い」の方が積立額は
少なくなる。
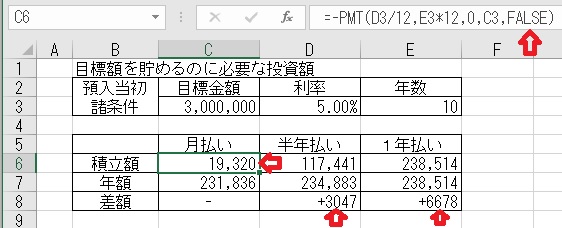
上図のセルC6に「=−PMT(D3/12,E3*12,0,C3,FALSE)」と入力すると、
「期末払い」の計算になる。この場合「後払い」のかたちになるので、
「月払い」より「半年払い」や「年払い」の方が、積立額を多く払う事になる
ので「月払い」の方が得する計算になる。
268.PMT関数で、目標額を貯めるのに必要な積立額を求める。

上図のセルC23に、
「=(B20*D20*12)+B20*C20/12*(D20*12+1)*D20*12/2」と入力する
と、「単利型」の満期額が求められる。
「単利型」は毎月の積立額をそれぞれ、満期までの残り月数での利息を計算する
考え方である。
満期額は、「(積立額×月利)×(月数+1)×月数÷2」として計算できるので、
「積立額×満期までの残月数×月利」と計算している。
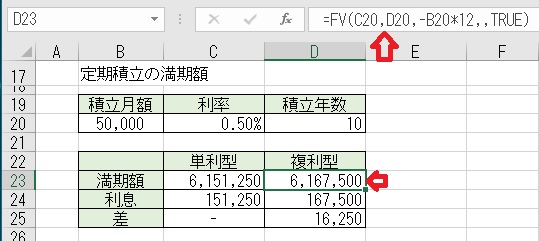
上図のセルD23に、「=FV(C20,D20,−B20*12, ,TRUE)」と入力すると、
「複利型」の満期額が求められる。
「1年複利」は、毎月の積立額に「12」を掛けて1年分をまとめて計算したのが
上図の数式である。
FV関数の第3引数に、「定期支払額」を指定することで、積立の計算ができる。
尚、「定期支払額」を指定する場合は、第5引数の「支払期日」を指定する
必要があり、「TRUE」として「機首払い」を指定すると、初回積み立て分か
ら利息を計算する。
「支払期日」は、一般的に利息が付いて満期額を受け取るので、「TRUE」か
「1」を指定する。
尚、第4引数は、「現在価値」で、将来価値として最後の支払いを行った後に
残る金額のことで、今は最後ではないので、「空白」か「0」を指定する。
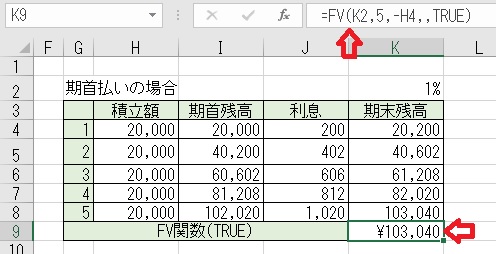
上図は、「支払期日」を「機首払い」に指定する場合の例である。
セルK9に「=FV(K2,5,−H4, ,TRUE)」と入力すると、期末残高が計算される。
「期末残高」の計算とFV関数による計算結果が合致することが分かる。
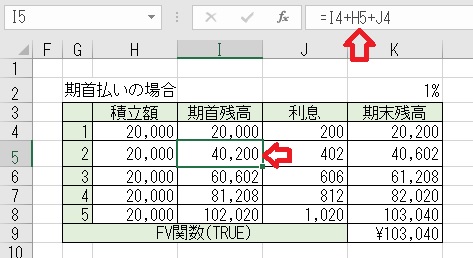
上図の様に
「当月の期首残高」=「前月の期首残高」+「当月の支払額」+「前月の利息」と
なる。
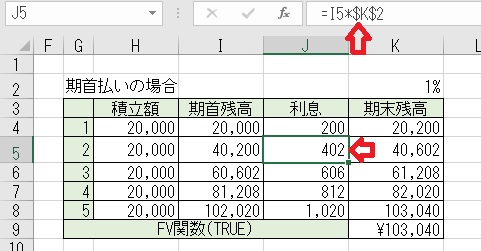
上図の様に「当月の利息」は、「当月の期首残高」×「利率」となる。
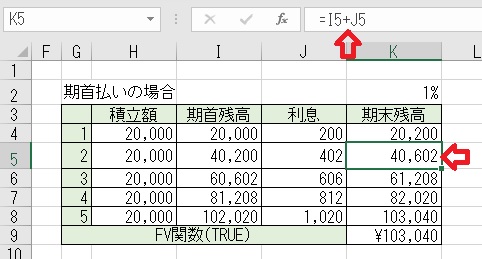
上図の様に「当月の期末残高」は「当月の期首残高」+「当月の利息」となる。
267.FV関数で、毎月の積立額から満期額を求める。
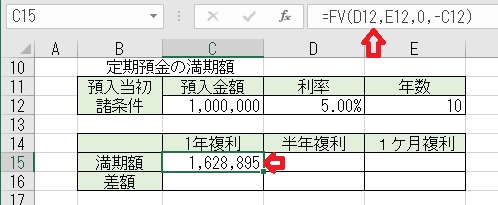
上図のセルC15に、「=FV(D12,E12,0,−C12)」と入力すると、「1年複利」の
満期額が算出される。
FV関数の書式は、「=FV(利率,期間,定期支払額,現在価値)」の様になっていて、
「現在価値」の部分には当初の預入金額を指定する。
但し、FV関数をはじめとする財務関数では、原則として収入はプラス、支出は
マイナスとして扱うため、当初の預入金額はマイナスとして指定する。
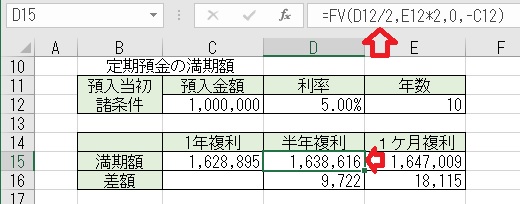
上図のセルD15に、「=FV(D12/2,E12*2,0,−C12)」と入力すると、「半年
複利」の満期額が算出される。利率は、「年利÷2」年数は、「年数×2」と
年2回なので月数を2倍にしている。定期支払額はないので「0」となる。
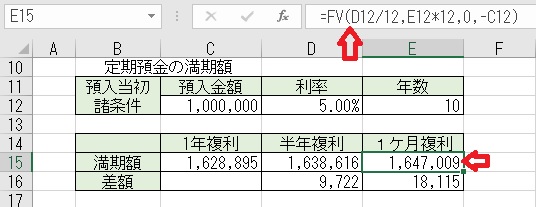
上図のセルE15に、「=FV(D12/12,E12*12,0,−C12)」と入力すると、
「1ケ月複利」の満期額が算出される。
利率は、「年利÷12」として月利に直し、利息は毎月計算されるので、
「年数×12」として月数を求める。このように「利率」と「期間」の単位を
合わせて指定する。
266.FV関数で、定期預金の満期額を求める。
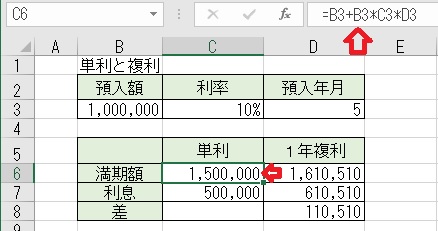
上図のセルC6に、「=B3+B3*C3*D3」と入力すると、「単利」の計算が
できる。「単利」は、「元金×年利×預入年数」として計算できる。
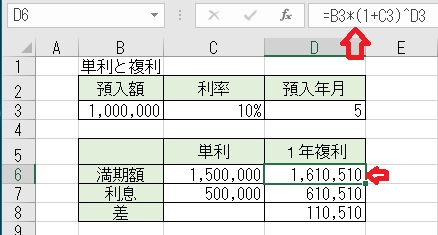
上図のセルD6に、「=B3*(1+C3)^D3」と入力すると、「複利」の計算が
できる。「複利」は、前期分の利息を元金に組み込んで、元利合計に対して
次期の利息を計算する。だから複利の場合は、元金もどんどん増えてゆく。
複利の場合の元利合計は、「元金×(1+金利)^年数」となる。
265.単利と複利の計算
XIV.金銭の計算
この章では、金銭にまつわる様々な計算に、財務関数を利用して行う方法を
解説をします。
関数の実用事例と引数の解説
金銭にまつわる計算に、財務関数を利用する方法の解説
必要な時に応用できる
EXCEL ワークシート関数 講座


























































































